Capitolo 2 Commento alla presentazione

La presentazione segue per sommi capi le prime due lezioni del capitolo II del libro Fourier Analysis and Applications di C. Gasquet e P. Witomski, oggetto della ricerca. Le slide sono autonome da un punto di vista teorico e possono essere utilizzate parallelamente al libro sopracitato come strumento supplementare per l’apprendimento.

Funzionalità

Le animazioni sono integrate nella presentazione ed è possibile interagire con esse;
formule, teoremi (o corollari) ed esempi sono demarcati rispettivamente con colore azzurro, verde e giallo per un più semplice riconoscimento;
formule e teoremi vengono visualizzati in una piccola scheda al passaggio o click del mouse sui rispettivi riferimenti, rendendo immediata la loro consultazione, mentre un ulteriore click su tali schede conduce alla slide in cui sono stati introdotti;

2.1 Segnali trigonometrici

Diciamo polinomi trigonometrici le funzioni del tipo

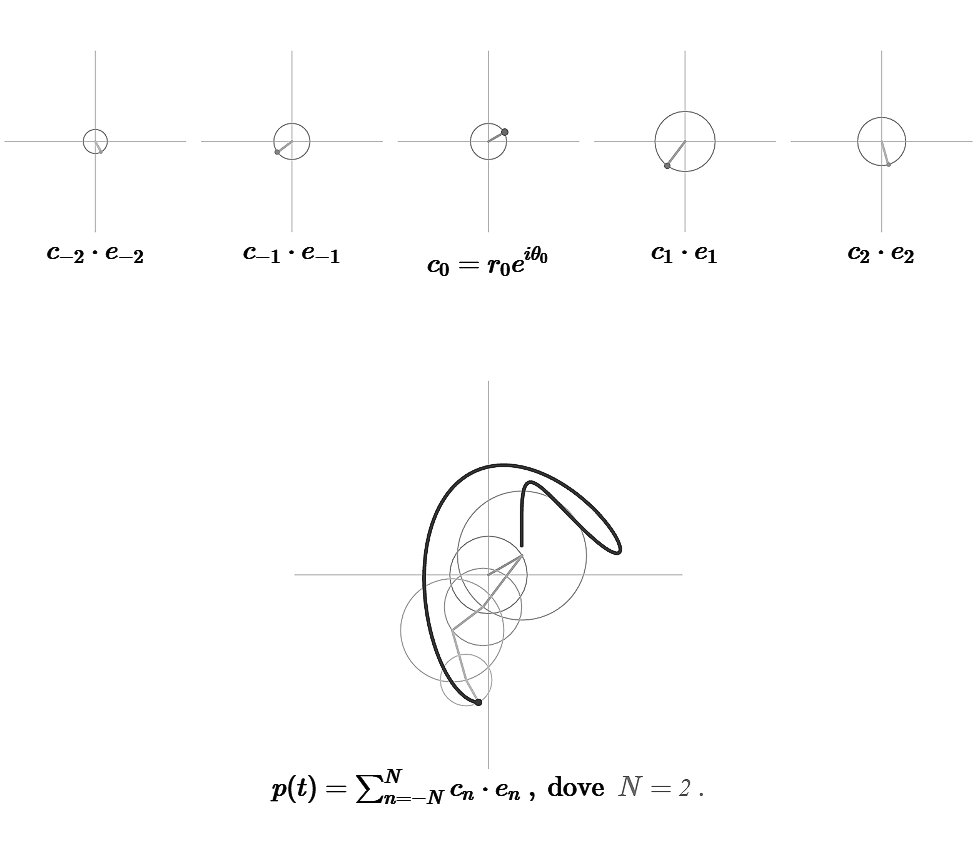
\[\begin{equation} p(t) = \sum_{n=-N}^N c_n e^{2 i \pi n \textstyle \frac {t}{a}} \ , \tag{2.1} \end{equation}\]

dove \(a,t \in \mathbb{R}, \ c_n \in \mathbb{C}\). \(p(t)\) ha periodo \(a\) e grado minore o uguale a \(N\).

Seguono immediatamente due animazioni per visualizzare un polinomio trigonometrico.

Nella prima è possibile - tramite rotella del mouse o trascinamento verticale su schermo - costruire progressivamente un polinomio trigonometrico aumentandone il grado e, di conseguenza, il numero di addendi.
Il primo elemento visibile è il coefficiente \(c_0\), ovvero un numero complesso. Gli altri elementi sono costituiti dal coefficiente complesso \(c_n\) moltiplicato per \(e_n(t)=e^{2\pi in\frac{t}{a}}\) ovvero la curva chiusa complessa con supporto la circonferenza unitaria, percorsa con frequenza \(n\). Poiché la moltiplicazione di due numeri complessi può essere interpretata come il multiplo di una rotazione, \(c_n \cdot e_n(t)\) rappresenta la curva chiusa con supporto una circonferenza di raggio \(|c_n|\) e una fase \(arg(c_n)=\theta_n\) (dove \(c_n=r_{n}e^{i\theta_n}\)) rispetto alla curva \(|c_n| \cdot e_n(t)\).
Le varie componenti del tipo \(c_n \cdot e_n(t)\) possono essere sommate con la definizione usuale di somma in campo complesso, ottenendo una curva che rappresenta proprio il polinomio trigonometrico.

Nella seconda animazione è possibile - sempre tramite rotella del mouse o trascinamento verticale su schermo - rivelare l’asse della variabile \(t\) per mezzo di una rotazione tridimensionale, visualizzando il polinomio trigonometrico nello spazio \(\mathbb{R} \times \mathbb{C}\).

Introduciamo quindi \(T_n\), spazio vettoriale (di dimensione \(2N-1\)) dei polinomi trigonometrici \(p(t)\) di grado minore o uguale a \(N\), dotato del prodotto scalare \[(p,q) = \int_{0}^{a} p(t) \overline{q}(t)dt \ .\] Da \((p,n)=a\cdot c_n\) ricaviamo quindi la formula di Fourier

\[\begin{equation} c_n=\frac{1}{a} \int_{0}^{a}p(t)e^{-2 i \pi n \textstyle \frac {t}{a}}dt \ . \tag{2.2} \end{equation}\]

Ci poniamo dunque la domanda fondamentale:

se \(f: \mathbb{R} \longrightarrow \mathbb{C} \ \) è una funzione arbitraria di periodo \(a\), possiamo trovare una decomposizione di \(f\) della forma \[\begin{equation} f(t) = \sum c_n e^{2 \pi in\textstyle \frac{t}{a}} \ , \tag{2.3} \end{equation}\] sotto minime ipotesi su \(f\) ?

2.2 Segnali periodici e serie di Fourier

In un celebre articolo del 1807, Joseph Fourier afferma che la risposta a tale domanda è affermativa, a patto che siano consentite somme infinite.

È possibile ridefinire questa risposta con gli strumenti della matematica moderna.
Per farlo, introduciamo lo spazio \[L_{p}^2(0,a)= \{ f:\mathbb{R} \longrightarrow \mathbb{C} \ : \ f \ \text{ ha periodo } a \text{ e } \int_{0}^{a}|f(t)|^2dt < +\infty\bigg\}\]

che, dotato delle usuali operazioni, è uno spazio vettoriale. Definiamo quindi il prodotto scalare \[(f,g) = \int_{0}^{a} f(t) \overline{g}(t)dt \ ,\]

e la norma associata \[ \Vert f \Vert_2 = \left( \int_{0}^{a} |f(t)|^2 dt \right) ^{\textstyle \frac{1}{2}} \ .\] Per rispondere alla domanda fondamentale occorre trovare l’elemento \(f_N\) nel sottospazio \(T_n\) di \(L_{p}^{2}(0,a)\) che ha la minima distanza da \(f\). Se esiste, lo chiamiamo la miglior approssimazione di \(f\) in \(T_{n}\).
La soluzione è fornita dal seguente teorema:

Teorema

Esiste un unico polinomio trigonometrico \(f_N\) in \(T_n\) tale che \[ \Vert f - f_N \Vert _{2} = \min_{p \in T_N} \Vert f - p \Vert _{2} \] Questo polinomio è dato da \[\begin{equation} f_{N}(t)=\sum_{n=-N}^{N} c_{n}e^{2\pi in \textstyle \frac {t}{a}} \ , \tag{2.4} \end{equation}\] dove \[\begin{equation} c_n=\frac{1}{a} \int_{0}^{a}f(t)e^{-2 i \pi n \textstyle \frac {t}{a}}dt \ . \tag{2.5} \end{equation}\]

Per qualunque \(f \in L_{p}^{2}(0,a) \ \), vale poi la disuguaglianza \[ \sum_{n=-\infty}^{\infty} |c_n|^{2} < + \infty \] e quindi \[ c_n(f) \rightarrow 0 \ \text{ per } \ |n| \rightarrow + \infty \ . \]

Il passaggio successivo consiste nello studio della convergenza.
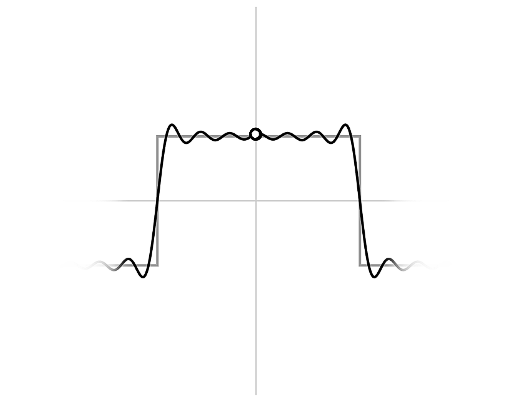
Grazie ad un esempio animato, è possibile osservare come l’approssimazione, data da una somma di seni, tenda alla funzione onda quadra:

è possibile - tramite rotella del mouse o trascinamento verticale su schermo - aumentare in numero di addendi nella somma e, quindi, migliorare l’approssimazione.

In conclusione, è possibile scrivere:

\[\begin{equation} f(t) = \sum_{n= - \infty}^{+ \infty} c_n e^{2 i \pi n \textstyle \frac {t}{a}} \ . \tag{2.6} \end{equation}\]

Si noti che questa è un’equivalenza nella norma di \(L_{p}^{2}(0,a)\) e non significa che, per qualunque valore di \(t\), \(f(t)\) sia uguale alla somma della serie.

2.3 Rappresentazione puntuale

Poiché una funzione impiegata in computazione numeriche è necessariamente valutata solo in un numero finito di punti, è importante determinare se la formula (2.6) possa esprimere un’equivalenza ad un dato punto \(t\).
Questo è il problema della convergenza puntuale.

Per risolverlo, ci dovremo estendere oltre \(L^2_p(0,a)\).

Dalla caratterizzazione dell’integrale di Lebesgue \[ f \text{ è Lebesgue-integrabile su } I \ \iff \ \int_{I}|f(t)|dt < +\infty \] segue immediatamente che i coefficienti di Fourier esistono se e solo se \(f\) è integrabile su \((a,b)\). Introduciamo la notazione \[L_{p}^{1}(0,a) = \left\{ f : \mathbb{R} \longrightarrow \mathbb{C} \ : \ f \text{ ha periodo } a \text{ e } \int_{0}^{a}|f(t)|dt < +\infty \right\} \ .\] e notiamo che \(L_p^2(0,a) \subset L_p^1(0,a)\), quindi \(f \in L_p^1(0,a)\) è una condizione meno restrittiva di \(f \in L_p^2(0,a)\).

Al momento non sappiamo se la serie \(\sum_{n=-\infty}^{+\infty}c_n(f)e^{2\pi in\frac{t}{a}}\) converga e, in caso di convergenza, non conosciamo il valore del limite.
Una condizione necessaria ma non sufficiente è che \[c_n \rightarrow 0 \text{ per } |n| \rightarrow + \infty \ .\] Tale condizione è verificata per \(f \in L_p^2(0,a)\) e rimane vera anche per \(f \in L_p^1(0,a)\)

Teorema di Riemann-Lebesgue

Sia \((a,b)\) un intervallo limitato e sia \(f\) integrabile su \((a,b)\). Allora l’integrale \[ I_n = \int_{a}^{b}f(x)e^{2 \pi in x} dx \rightarrow 0 \ \text{ per } \ |n| \rightarrow + \infty \]

Un altro importante risultato è riassunto dal teorema di Dirichlet, che mostra come la convergenza della serie di Fourier di \(f\) in un punto \(t_0\) dipende esclusivamente dal comportamento di \(f\) in un intorno di \(t_0\).

Teorema di Dirichlet

Sia \(f \in L^1_p(0,a)\). Se esistono i limiti \(f(t+)\) e \(f(t-)\) in un punto \(t_0\)
ed esistono le derivate destra e sinistra in \(t_0\), allora \[f_N(t_0) \rightarrow \frac{1}{2} \big[ f(t_0+) + f(t_0-) \big] \ \text{ per } \ N \rightarrow +\infty \ .\] Se \(f\) è continua in \(t_0\), \(f_N(t_0) \rightarrow f(t_0)\).

È infine possibile ricavare delle informazioni in merito alla convergenza uniforme:

Proposizione

Se \(f \in L^2_p(0,a)\) e i suoi coefficienti di Fourier soddisfano \[ \sum_{n=-\infty}^{\infty} |c_n| < + \infty \ ,\] allora \(f\) è uguale q.o. ad una funzione continua \(\tilde f\) e la serie di Fourier di \(f\) converge uniformemente a \(\tilde f\) su \(\mathbb{R}\).

In chiusura, vengono proposte le due animazioni riassuntive che riguardano un peculiare esempio:

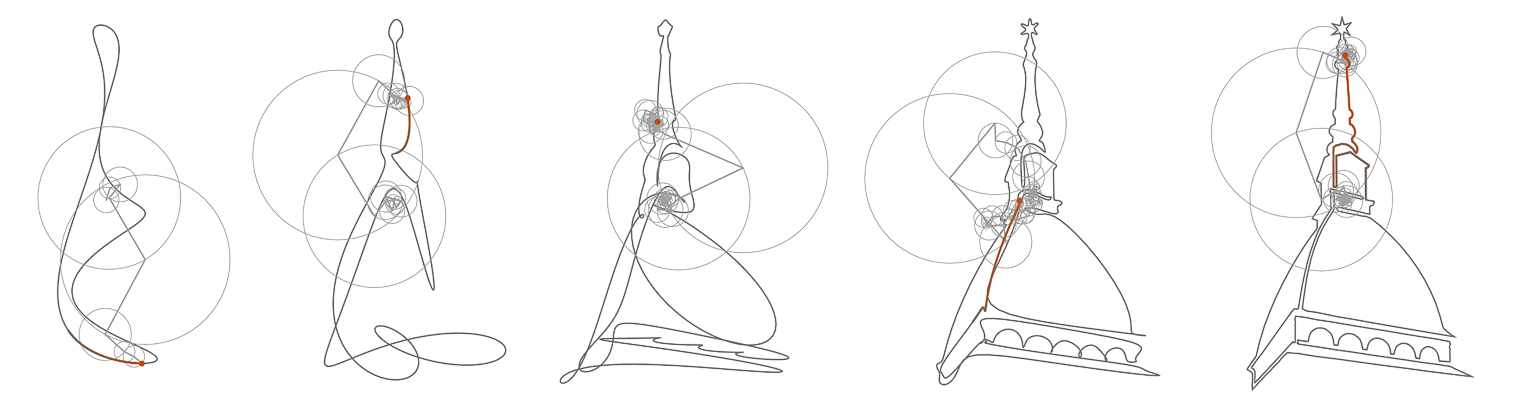
la prima, la più importante di tutta la presentazione, mostra la convergenza puntuale alla funzione \(f\) della sua serie di Fourier. È possibile - tramite rotella del mouse o trascinamento verticale su schermo - migliorare l’approssimazione data dalla somma parziale \(N\)-esima della serie di Fourier, facendo variare \(N\). È inoltre visibile, nella parte superiore, lo spettro del segnale periodico \(f\), definito dall’insieme di coppie \((n/a,c_n), \ n \in \mathbb{Z}\) dove \(c_n\) è l’\(n\)-esimo coefficiente di Fourier di \(f\).
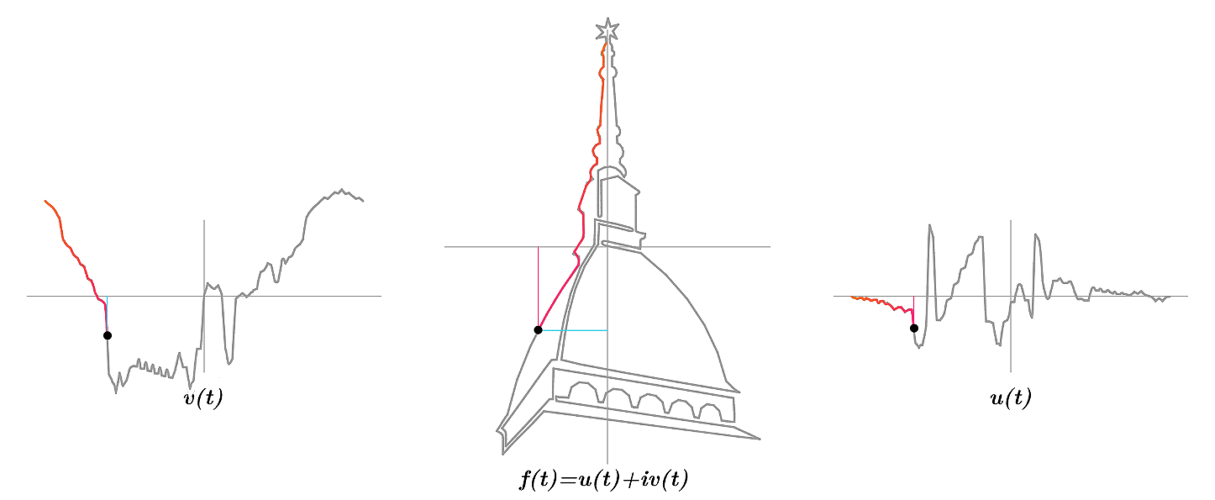
la seconda mette in evidenza, tramite la scomposizione di \(f(t)\) in \(f(t)=u(t)+iv(t)\), la continuità di \(f\) e la sua appartenenza a \(L^1_p(0,a)\);